4883번: 삼각 그래프
입력은 여러 개의 테스트 케이스로 이루어져 있다. 각 테스트 케이스의 첫째 줄에는 그래프의 행의 개수 N이 주어진다. (2 ≤ N ≤ 100,000) 다음 N개 줄에는 그래프의 i번째 행에 있는 정점의 비용이
www.acmicpc.net
문제 풀이
이번 문제는 DP 문제이다. 이 문제의 경우, 가장 위쪽 가운데 정점에서 가장 아래쪽 가운데 정점으로 가는 최단 경로를 찾아야 한다.
규칙 찾기
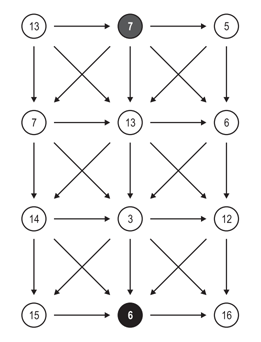
그림을 보면, 각 정점 사이의 간선들은 화살표로 표시되고 있다. 일방통행으로, 반대로 갈 수는 없기 때문에, 각각의 정점 별 최선의 경로를 찾아볼 수 있다.

먼저, 3열의 왼쪽 정점들은 위 그림과 같이 두 개의 경로에서 내려올 수 있다. 따라서 두 경로 중 낮은 비용의 경로를 선택하면 된다.

3열의 중앙 정점들은 총 4개의 경로가 존재한다. 4가지의 경로 중 가장 낮은 비용의 경로를 선택하면 된다.

마지막으로 3열의 오른쪽 정점들은 총 3개의 경로가 존재한다. 3가지의 경로 중 가장 낮은 비용의 경로를 선택하면 된다.
입력값들을 순차적으로 그래프에 담아준 뒤, 1행부터 DP 규칙을 통해 끝까지 비용을 계산해주면 답을 구할 수 있다.
예외 처리
초기 설정이 중요하다. 무조건 출발 정점은 맨 위 가운데 정점이므로 맨 위 행의 왼쪽 부분의 값을 초기에 변경해주어야 한다. 예를 들어 입력값이
2
1 2 3
4 5 6일 경우, DP의 규칙으로만 따진다면, 2번째 행의 왼쪽 정점은 1번째 행의 왼쪽 정점의 값을 받기 때문에, 입력빋는 정점의 비용보다 더 큰 값을 맨 위 왼쪽 정점에 입력해주어야 한다.
정답 코드
#include <iostream>
#include <cstring>
#include <algorithm>
#include <vector>
#include <cmath>
using namespace std;
#define fast ios_base::sync_with_stdio(false); cin.tie(0), cout.tie(0)
#define ll long long
int dp[100001][3];
int main() {
fast;
int cnt = 1;
while (1) {
int N;
cin >> N;
if (N == 0) break;
for (int i = 0; i < N; i++) cin >> dp[i][0] >> dp[i][1] >> dp[i][2];
dp[0][0] = 987654321;
dp[0][2] += dp[0][1];
for (int i = 1; i < N; i++)
{
dp[i][0] = min(dp[i - 1][0], dp[i - 1][1]) + dp[i][0];
dp[i][1] = min(min(dp[i - 1][0], dp[i][0]), min(dp[i - 1][1], dp[i - 1][2])) + dp[i][1];
dp[i][2] = min(dp[i - 1][1], min(dp[i - 1][2], dp[i][1])) + dp[i][2];
}
cout << cnt << ". " << dp[N - 1][1] << "\n";
cnt++;
}
}그래프 입력과 dp 배열을 하나로 계속 사용해서 메모리 사용을 줄일 수 있었다.
'Algorithm > PS' 카테고리의 다른 글
| [C++, python] BOJ, 백준 5569 - 출근 경로 (0) | 2023.02.23 |
|---|---|
| [C++, python] BOJ, 2502 - 떡 먹는 호랑이 (0) | 2023.02.22 |
| [C++, python] BOJ, 백준 1577 - 도로의 개수 (0) | 2023.02.22 |
| [C++, PYTHON] BOJ, 백준 5582 - 공통 부분 문자열 (0) | 2023.02.22 |
| [C++] BOJ, 백준 2011 - 암호코드 (0) | 2023.02.20 |
